Material Properties: Silicon
Data Available:
- Thermal Expansion Coefficient
Silicon thermal expansion coefficient
High purity silicon (single crystal any direction or polycrystalline) is used as a standard reference material for the thermal expansion coefficient from 10 K to 1300 K [1]. We have included two more recent measurements of high accuracy in the fit given here. Because of the extensive and high-accuracy data available on the thermal expansion coefficient of silicon, our fitting equation includes more coefficients than those used with most other materials on our web site. Deviations between the curve fit and data are generally less than the uncertainty of the data. However, this curve fit should not be considered a fit officially approved by any standards organization. The use of the error functions in the curve fit here allow for a smooth blending of fits over different temperature ranges. As a result the equation given here is good from 0 K to 600 K.
[1] G.K. White and M.L. Minges, “Thermophysical Properties of Some Key Solids: an Update,” International Journal of Thermophysics 18, No. 5 (1997) pp. 1269-1327.
Thermal Expansion Coefficient |
|
| UNITS | 10-8 / K |
| a | 1.00500E-05 |
| b | -5.99688E-06 |
| c | 1.25574E-06 |
| d | -1.12086E-07 |
| e | 3.63225E-09 |
f |
2.67708E-02 |
g |
-1.22829E-04 |
h |
1.62544E-18 |
i |
4.72374E+02 |
j |
-3.58796E+04 |
k |
-1.24191E+07 |
l |
1.25972E+09 |
data range |
13-600 K |
equation range |
0-600 K |
curve fit standard error relative to data |
0.03x10-8 (T < 50K); 0.5x10-8 (T ≥ 50K) |
Thermal Expansion Coefficient Given: |
|
The curve fit for thermal expansion coefficient, a Solves as: |
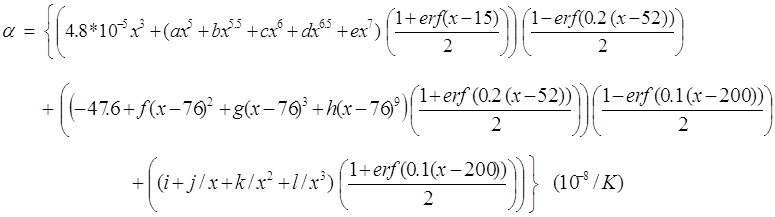 |
| Where: |
|
| NOTE: | The error function (sigmoid shape) is used to blend fits over separate temperature ranges. |
The error function ‘erf(x)’ (also known as the Gauss error function) is defined as:
(When x is negative, the integral is interpreted as the negative of the integral from x to zero.) In Excel the error function may be calculated by employing the following format ‘ERF( lower_limit, upper_limit)‘ or simply ‘ERF(value of x)‘. For example ERF(0, 1.5) = ERF(1.5) which results in the integral of error function between 0 and 1.5. Excel 2010 and later evaluate correctly for both possitive and negative values of x. Whereas earlier versions can only evaluate for positive values of x (ie x > 0). Thus one must employ –ERF(x) = ERF(-x) to evaluate negative values of x properly in earlier versions of Excel (prior to 2010). |
