
The example is for fitted vapor pressures for benzene.
Listed below are the properties for which evaluated data is generated by TDE. Each property is linked to a list showing the set of possible equations that can be fit to the data. The equation that is used for a specific query is the one that provides the best fit of the data. This equation is then used to provide evaluated data.
NOTE: All of this information is displayed here in an individual file so that you can do text searches by using the Find funtion from the Edit menu of your browser.
Purpose: Provide definitions of equations and equation parameters used for output of evaluated data.
Select a property to see all associated equations. Properties represented with equations in TDE output are:
ln(p/po) = a + b/T + c×ln(T) + d×T2 + e/T2 ; where po = 1 kPa
ln(p/po) = a + b/T + c×ln(T) + d×Te ; where po = 1 kPa
ln(p/po) – ln(pc/po) = Tc/T (A1 + A2×t1.5 + A3×t3 + A4×t6); where t = 1 - T/Tc and po = 1 kPa
Evaluation Results:

The example is for fitted vapor pressures for benzene.
Evaluation Results:

The example is for fitted vapor pressures for benzene.
Evaluation Results:

The example is for fitted vapor pressures for benzene.
Evaluation Results:

The example is for fitted vapor pressures for benzene.
Evaluation Results:

The example is for fitted vapor pressures for benzene.
Evaluation Results:

The example is for fitted vapor pressures for benzene.
ln(p/po) = a1 + a2/T + a3×ln(T) + a4×T + a5×T2 + a6×T6+ a7/T4
ln(p/po) = A + B/(T + C); where po = 1 kPa
lg(p/po) = a + b/T + c×lg(T) + d×T + e/T2 ; where po = 1 kPa and lg = log10
ln(p/po) = a + b/T + c×ln(T) + d×T2 + e/T2 ; where po = 1 kPa
ln(p/po) = a + b/T + c×ln(T) + d×Te ; where po = 1 kPa

NOTE: The TDE program truncates this equation based upon the extent and quality of the fitted data.
ln(p/po) = å ai× T i, where the summation is from i = 0 to nTerms - 1
Evaluation Results:

The example is for fitted phase-boundary pressures for benzene.
dsat = dc + a1×t0.35 + åai+1×ti , where the summation is from i = 1 to nTerms -1.
dc = the critical density and t = 1 - T/Tc, where Tc is the critical temperature.
dc = the critical density and t = 1 - T/Tc, where Tc is the critical temperature.

NOTE: The TDE program truncates this equation based upon the extent and quality of the fitted data.

dc = the critical density and t = 1 - T/Tc, where Tc is the critical temperature.
Evaluation Results:

The example is for fitted densities at vapor saturation for benzene.
Evaluation Results:

The example is for fitted densities at vapor saturation for benzene.
dsat = dc + a1×t0.35 + åai+1×ti , where the summation is from i = 1 to nTerms -1.
dc = the critical density and t = 1 - T/Tc, where Tc is the critical temperature.
d = dsat / [1 - c×ln{(b + p) / (b + psat)}] ; where
b = åBi+1×t i,
c = åCi+1×t i, and
t = (T-Tcenter)/100, where Tcenter is a constant parameter.
Summations are from i = 0 to (nTerms -1), where nTerms is the number of B or C terms.
dsat = the density of the saturated liquid and psat = the saturation vapor pressure.
b = åBi+1×t i,
c = åCi+1×t i, and
t = (T-Tcenter)/100, where Tcenter is a constant parameter.
Summations are from i = 0 to (nTerms -1), where nTerms is the number of B or C terms.
dsat = the density of the saturated liquid and psat = the saturation vapor pressure.

d = 1000×Mw / Vm; where Mw is the molar mass and Vm is the molar volume.
Z = 1000×p×Vm/(R×T) = 1 + B/Vm + C/Vm2,
where B = åbi+1/T i and C = åci+1/T i
Z = 1000×p×Vm/(R×T) = 1 + B/Vm + C/Vm2, where B = åbi+1/T i and C = åci+1/T i
Evaluation Results:

The example is for fitted gas densities of pentane.
ln(Hvap/Hvapo) = a1 + åai ×Tri-1×ln(1-Tr) , where the summation is from i = 2 to nTerms -1
Tr = T/Tc, Tc is the critical temperature, and Hvapo = 1 kJ/mol
Hvap = A×{1 - ( T / Tc )}n
Hvap/R = a1×t1/3 + a2×t2/3 + a3×t + a4×t2 + a5×t6
where t = 1 - T/Tc, Tc is the critical temperature, and R is the gas constant.
Tr = T/Tc, Tc is the critical temperature, and Hvapo = 1 kJ/mol
Evaluation Results:

The example is for fitted enthalpies of vaporization for benzene.
Evaluation Results:

The example is for fitted enthalpies of vaporization for pentane.
where t = 1 - T/Tc, Tc is the critical temperature, and R is the gas constant.
Evaluation Results:
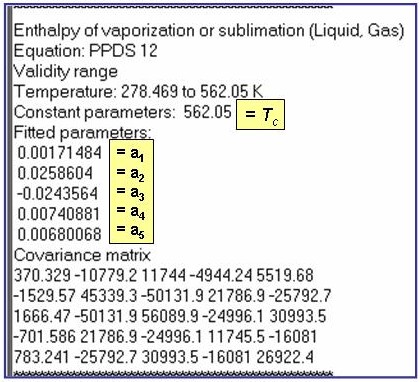
The example is for fitted enthalpies of vaporization for benzene.
Csat = (åai+1× ti) + b/t , where the summation is from i = 0 to nTerms -1.
Csat = å ai× T i, where the summation is from i = 0 to nTerms - 1
Csat = å ai× T i, where the summation is from i = 0 to nTerms - 1
Csat / R = a0/t + a1 + a2×t + a3×t2 + a4×t3 + a5×t4
where t = 1 - T/Tc, Tc is the critical temperature, and R is the gas constant.
Evaluation Results:

The example is for fitted heat capacities at vapor saturation for benzene.
Evaluation Results:

The example is for fitted heat capacities at vapor saturation for benzene.
Evaluation Results:

The example is for fitted heat capacities at vapor saturation for benzene.
where t = 1 - T/Tc, Tc is the critical temperature, and R is the gas constant.
Evaluation Results:

The example is for fitted heat capacities at vapor saturation for benzene.
Cpo = å ai× T i, where the summation is from i = 0 to nTerms - 1
Cpo = a + b×{(c/T)/sinh(c/T)}2 + d×{(e/T)/cosh(e/T)}2
Cpo/R = Clow + (Clow - C¥)×y2 ×{1 + (y - 1) å(ai × yi)} ; where the summation is from i = 0 to 4.
Clow and C¥ are equation constants, and y = T / (T + TS), where TS is a constant.
Cpo/R = 1 + t - {åai×ni×(ni - 1)×tni}(ni¹ 0 or 1) + åbi×(ci×t)2×exp(ci×t) / {exp(ci×t) - 1}2;
where t = Tc/T, Tc = the critical temperature,
and the summations are from i = 1 to nTerms.

The example is for fitted heat capacities in the ideal-gas state at p = 100 kPa for pentane.
Reference: Aly, F. A.; Lee, L. L. Fluid Phase Equil. 1981, 6, 169-179.
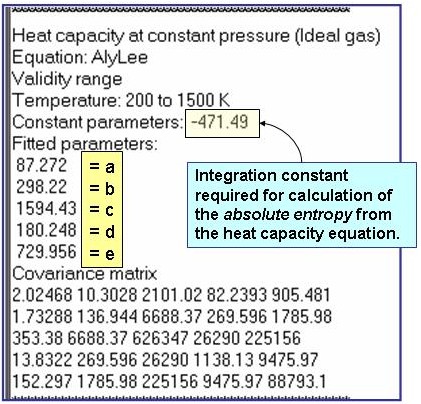
The example is for fitted heat capacities in the ideal-gas state at p = 100 kPa for pentane.
Clow and C¥ are equation constants, and y = T / (T + TS), where TS is a constant.
Evaluation Results:
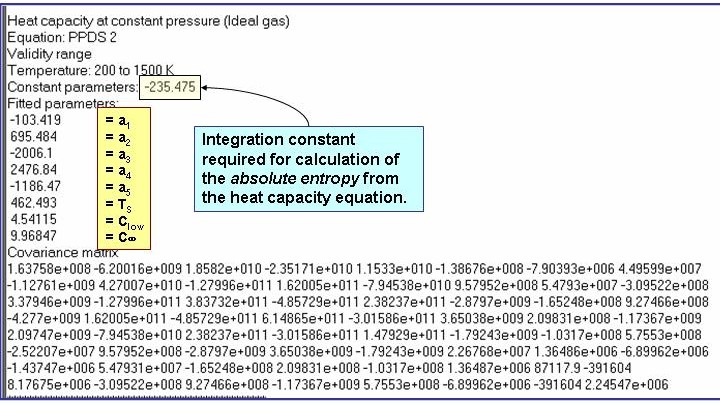
The example is for fitted heat capacities in the ideal-gas state at p = 100 kPa for pentane.
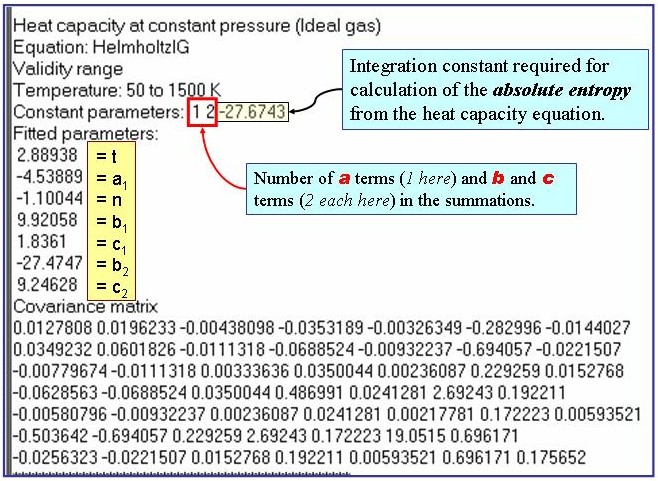
u = A + B×T + C×(d - dsat) + D×d 2,
where d is the density of the liquid and dsat is the density of the saturated liquid.
where d is the density of the liquid and dsat is the density of the saturated liquid.

The example is for fitted speeds of sound for benzene.
u = A + B×T + C×p + D×p/T ;
where T is the temperature and p is pressure.
where T is the temperature and p is pressure.

The example is for fitted speeds of sound for pentane in the gas phase.
nD = A + B×t + å Ci×wi ;the summation is from i = 1 to nTerms
where t = T - 298.15 K and w = WL - 589.26 (WL = wavelength in nm)
where t = T - 298.15 K and w = WL - 589.26 (WL = wavelength in nm)
Evaluation Results:

The example is for fitted surface tensions for pentane.
s = a0× ta1×(1 + a2 ×t) , where t = 1 - T/Tc and Tc is the critical temperature.
s = exp(A)×{1 - ( T / Tc )}n
ln(s/so) = a1 + åai ×Tri-1×ln(1-Tr) , where the summation is from i = 2 to nTerms -1
Tr = T/Tc, Tc is the critical temperature, and so = 1 N/m
Evaluation Results:

The example is for fitted surface tensions for benzene.
s = exp(A)×{1 - ( T / Tc )}n
Evaluation Results:

The example is for fitted surface tensions for benzene.
Tr = T/Tc, Tc is the critical temperature, and so = 1 N/m

The example is for fitted surface tensions for benzene.
ln(h/ho) = a1 ×X1/3 + a2 ×X4/3 + ln(a5) , where X = (a3 - T) / (T - a4) and ho = 1 Pa×s
lg(h/ho) = A + B/T + C×T + D×T 2
ln(h/ho) = a + b/T + c×ln(T) + d×Te ; where ho = 1 Pa×s
Evaluation Results:

The example is for fitted viscosities for the saturated liquid phase of benzene.
Evaluation Results:

The example is for fitted viscosities for the saturated liquid phase of benzene.
Evaluation Results:

The example is for fitted viscosities for the saturated liquid phase of benzene.
h = å ai× T i, where the summation is from i = 0 to nTerms - 1
h = å ai× T i, where the summation is from i = 0 to nTerms - 1
h = A×T B / (1+ C/T + D/T 2)
h = a0×Tr / {1 + a1×(Tr - 1)× Tra2}1/6; where Tr = T/Tc and Tc is the critical temperature.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of pentane.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of pentane.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of pentane.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of pentane.
l = å ai× T i, where the summation is from i = 0 to nTerms - 1
lg(l/lo) = A + B×(1 - T/C)2/7
l = å ai× T i, where the summation is from i = 0 to nTerms - 1
l = å ai× T i, where the summation is from i = 0 to nTerms - 1
l = a1 + å(ai+1 ×ti/3) , where the summation is from i = 1 to nTerms -1 and t = 1 - T/Tc
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of benzene.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of benzene.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of benzene.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of benzene.
Evaluation Results:

The example is for fitted thermal conductivities for the liquid phase of benzene.
l = å ai× T i, where the summation is from i = 0 to nTerms - 1
l = å ai× T i, where the summation is from i = 0 to nTerms - 1
l = Tr0.5 (åai / Tri)-1 , where the summation is from i = 1 to 3,
and Tr = T/Tc, where Tc is the critical temperature.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of pentane.
Evaluation Results:
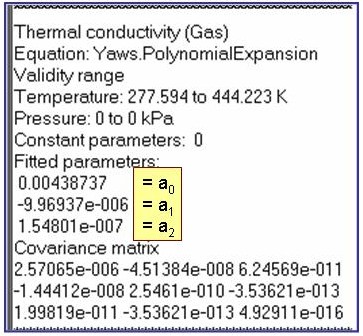
The example is for fitted thermal conductivities for the saturated liquid phase of pentane.
and Tr = T/Tc, where Tc is the critical temperature.
Evaluation Results:

The example is for fitted thermal conductivities for the saturated liquid phase of pentane.